 According to an old saying, there’s more than one way to skin a cat. There are at least as many ways to compute the value of π. One of them uses the Monte Carlo method to approximate π’s value and it is the subject of today’s Bug Hunting epsisode.
According to an old saying, there’s more than one way to skin a cat. There are at least as many ways to compute the value of π. One of them uses the Monte Carlo method to approximate π’s value and it is the subject of today’s Bug Hunting epsisode.
We start with a so-called unit circle, a circle with radius 1 whose center is positioned at the origin in the Cartesian coordinate system. Next, we put a square around the unit circle whose sides have length 2 (the diameter of the unit circle):
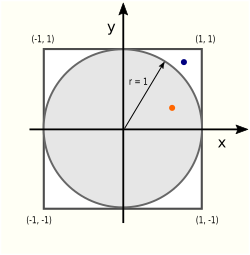 There are two areas (literally!) of interest in this picture: the circle area Ac and the square area As:
There are two areas (literally!) of interest in this picture: the circle area Ac and the square area As:
Ac = πr² = π
As = (2r)² = 4
The ratio Ac/As is π/4
Why is this ratio important? Because we can use it to calculate the value of π:
π = 4 Ac/As
Now let’s do some random sampling. We take N random points whose x and y values are both in range [-1; +1] and tally the number of points that fall within the square (Ns) and the number of points that fall within the circle (Nc). Given enough points, the ratio Nc/Ns is a very good approximation for Ac/As and we hence can compute:
π ≈ 4 Nc/Ns
The C code below attempts to calculate π in this manner, but sports a blunder. What is the bug? Bonus question for the mathematically inclined: without executing the code, what value does it really compute (instead of π)?