
— Aristotle
How time flies! More than two years have passed since I posted my last kata, so it’s high time for a new one. Today’s kata is based on a real problem that I had to solve last week when I worked on a code generator that produced C/C++ code. I hope you enjoy this task as much as I did!
When you define a struct in C, the overall size of the struct is not necessarily the sum of its members. Much like in real life, the whole is greater than the sum of the parts. Consider this example:
|
1 2 3 4 5 6 |
struct Foo { uint8_t a; uint32_t b; }; |
Only novice programmers would assume that sizeof(Foo) equals 5; experienced programmers know that 8 is a much safer bet. How come?
Most computer architectures can access data only if it is properly aligned in memory, e. g. a 32-bit (4-byte) integer can only be accessed if it is stored at an address that is evenly divisible by 4. The compiler usually achieves this by inserting invisible padding bytes between the struct members. Thus, internally, struct Foo is likely to look like this:
|
1 2 3 4 5 6 7 8 9 |
struct Foo_internal { uint8_t a; uint8_t _pad1; uint8_t _pad2; uint8_t _pad3; uint32_t b; }; |
As a first step, familiarize yourself with struct padding. Check out this must-read by legendary Eric S. Raymond, especially if you are a systems programmer.
Now that you have read it, you should understand why sometimes there is also trailing padding (but never leading padding) and hence why the size of the following struct is most likely 12:
|
1 2 3 4 5 6 7 |
struct Bar { uint8_t a; uint32_t b; uint8_t c; }; |
Equipped with this knowledge we are ready to tackle our first programming task: assume that every primitive struct member of base-2 size is to be aligned on its base-2 boundary (a 2-byte integer on an address that is evenly divisible by 2, a 4-byte integer on an address that is evenly divisible by 4 and so on). Implement an algorithm that computes the overall size of a struct given an ordered list of its members. Instead of real types, provide a list of integer values where the values represent the sizes of the members. Here are examples for Foo and Bar (in Python):
|
1 2 3 4 |
assert(struct_size([1, 4]) == 8) # Foo assert(struct_size([1, 4, 1] == 12) # Bar |
One weakness of this approach is that you cannot differentiate between a unit32_t (size is 4, alignment is 4) and an array of 4 uint8_ts (size is 4, alignment is 1):
|
1 2 3 4 5 6 7 |
struct Baz { uint8_t a; uint8_t b[4]; uint8_t c; }; |
Extend your algorithm to accept a list of pairs, where the first pair member specifies the size and the second pair member specifies the alignment:
|
1 2 3 4 5 |
assert(struct_size([(1, 1), (4, 4)]) == 8) # Foo assert(struct_size([(1, 1), (4, 4), (1, 1)] == 12) # Bar assert(struct_size([(1, 1), (4, 1), (1, 1)] == 6) # Baz |
But there is one more feature we need to add before we’re done: support for arbitrarily nested structs:
|
1 2 3 4 5 6 7 |
struct Fuz { uint8_t a; struct Foo b; uint8_t c; }; |
How does a member that itself is a struct impact the alignment of the outer struct? Devise a suitable data structure for passing in nested struct specifications.
[Update 2016-03-12: I’ve uploaded a sample solution to GitHub]
 Last month,
Last month, 
 According to an old saying, there’s more than one way to skin a cat. There are at least as many ways to compute the value of π. One of them uses the
According to an old saying, there’s more than one way to skin a cat. There are at least as many ways to compute the value of π. One of them uses the 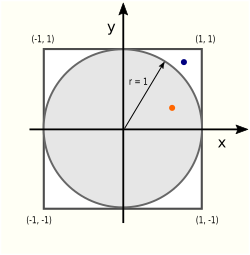 There are two areas (literally!) of interest in this picture: the circle area Ac and the square area As:
There are two areas (literally!) of interest in this picture: the circle area Ac and the square area As: